I presented a few online portfolio selection algorithms in my previos blogs (1, 2, 3, 4, 5). Here is a quick summary of the algorithms discussed so far:

Last Weekend, I participated in a Hackathon organized by Cubist and won first place! I got to work with some talented students from Yale, Cornell, and Columbia. Our project focused on enhancing ambulance staffing and stationing in New York City by analyzing geographic data of collisions and existing service locations/hospitals.

I presented the Smooth Selection(SS) algorithm in my previous blog. Assuming the stock returns are lower bounded by \(r\), the regret of SS is \(O(\frac{n}{r}\log(T))\), and the run time is \(O(n^{2.5} T)\) per iteration. In this blog, I present the Online Newton Step Algorithm that improves the runtime to \(n^{3.5}\).

I presented the Exponentiated Gradient(EG) algorithm in my previous blog. Assuming the stock returns are lower bounded by \(r\), the regret of EG is \(O(\frac{1}{r}\sqrt{T\log(n)})\) and the run time is \(O(n)\) per iteration. Using a standard trick for “universalizing”, we can remove the lower bound assumption and get a regret of \(O(n^{1/2}\log(n)^{1/4} T^{3/4})\). In this blog, I present the Smooth Prediction Algorithm that improves the dependence on \(T\) to \(O(\log T)\).

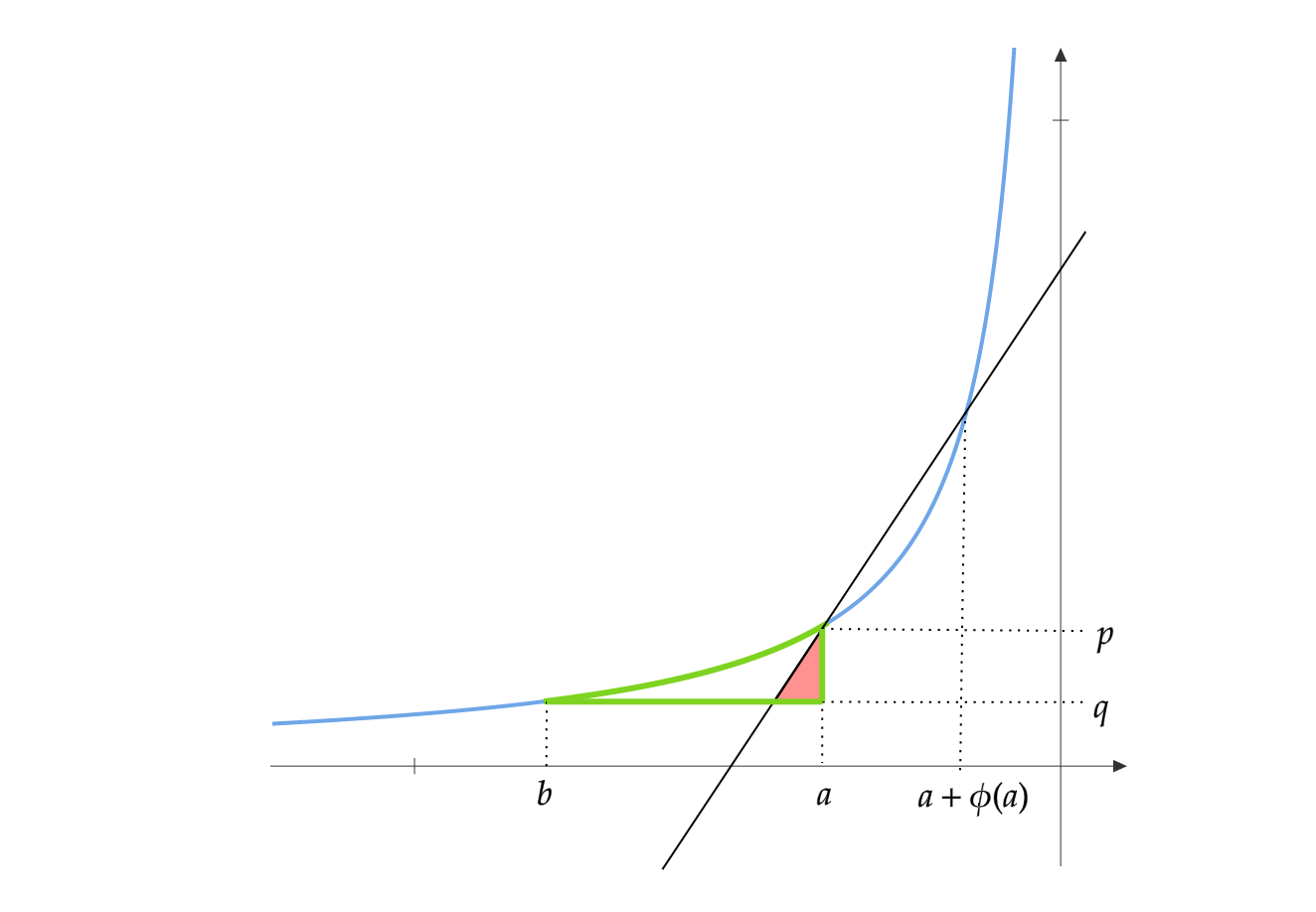
I presented Cover’s universal portfolio algorithm in my last blog. It has a regret bound of \(O(n \log T)\), where \(n\) is the number of stocks and \(T\) is the number of days traded. I implemented it for the case of two stocks. In the case of large \(n\), Cover’s algorithm can be run using a Markov Chain Monte Carlo simulation. The computation time for this scales as \(O(n^4 T^{14})\), which is quite prohibitive for even moderate \(n\) and \(T\). So, in this blog, I present a gradient descent-based algorithm that trades off computation time with regret bound while still staying universal.

In my last blog, I mentioned that a desirable feature of an online portfolio selection algorithm is minimax regret optimality, i.e., we want an algorithm \(Alg^\star\) satisfying:

I started working on Online Portfolio Selection after reading an open problem published in COLT 2020 - Open Problem: Fast and Optimal Online Portfolio Selection. I spent the next two years reading about online portfolios and portfolio theory from a theoretical and practical standpoint. In a series of blogs, I intend to write about this problem. For me, this problem was a gateway to learning more about concepts in both online learning and portfolio optimization.

The recent paper, Discovering faster matrix multiplication algorithms with reinforcement learning by DeepMind, has been garnering much attention from both the ML and TCS communities. The algorithm in the paper, called AlpaTensor, can find fast matrix multiplication algorithms for some fixed-size matrices. Some in the ML community hail it as yet another outstanding achievement for deep RL :

Over 6 years ago, I wrote a blog post on the Derivation of Backpropagation in Matrix Form. My toolkit then included a basic understanding of the chain rule, linear algebra, and checking the dimension. And so I set about writing that post. With some questionable usage of the chain rule, I derived the backpropagation equations. At every step, I told myself - The dimensions check out, so it must be correct. That post became the most popular blog I had ever written. It still brings in a few hundred visitors each week.

This post examines the mean of a Censored Poisson Distribution. The Poisson distribution has the probability mass funtion:

So far, we have shown how to get regret inequalities for OMD/FTRL where the second term is a sum, whose summands are of the form:

We have seen 3 online learning algorithms: 1-step OMD, 2-step OMD and FTRL. Usually FTRL is written and studied as a single step update. However, it is possible to define and analyze a 2-step version of FTRL as well.

Let \(\psi\) be a potential and \(f\) be the associated function. Define \(F(x)=\sum_{i=1}^n f(x_i)\).

Let \(\psi\) be a potential and \(f\) be the associated function. Define \(F(x)=\sum_{i=1}^n f(x_i)\). Define the Bregman Divergence as :

This post is about “Potential Functions” in the context of Online Learning. These form the basis for the Implicitly Normalized Forecaster(INF) studied in [1,2]. We present some basic results about potential functions here.

In this post, I document a few tricks that can be used to modify standard regret inequalities.

Consider the online linear optimization problem. At each round, the adversary chooses a loss function \(l_t \in \mathcal{F}\) and the player picks \(x_t \in \mathcal{K}\) from a convex set \(\mathcal{K}\). Roughly speaking, there are two basic settings in this problem:

This is a reference blog post about useful regularizers for Online Mirror Descent. This is by no means an exhaustive list. I have only added regularizers that I have seen in papers.

Let A be a \(n \times n\) positive semi-definite matrix. Let \(\lambda_1\geq \lambda_2 \geq \dots \geq \lambda_n\) be the eigenvalues in decreasing order and \(u_1,u_2,\dots,u_n\) be the corresponding orthonormal eigenvectors. We have

This post is a continuation of my previous posts on Online Learning. Here is a quick recap.

Let \(B=I_n+UV\), where \(U \in \mathbb{R}^{n \times m}\) and \(V \in \mathbb{R}^{m \times n}\) such that \(m>>n\). The goal is to find \(B^{-1}\). Using the Sherman–Morrison–Woodbury formula, we have:

In this blog post, we introduce OMD and state an upperbound for its regret. Using this upperbound, we analyze the regret of the algorithm we proposed in our previous blog.

In this post, we consider the Online Linear Optimization problem where the decision set is confined to the vertices of a Hypercube. Naively applying Hedge to this problem achieves optimal regret in \(T\) but requires maintaining an exponential number of variables. We show that it is in fact possible to apply Hedge by using only linear number of variables.

This blog is primarily about an easier way of understanding the Lovasz extension of submodular functions.

This is a continuation of my previous blog post on Hedge. Here we consider Bandit feedback instead of full information.

Assume you are a grad student taking two courses this semester. One of which is Machine Learning Theory, which is your favorite course. You don’t like the other course so much, so you never study for it. You still have to do well in this course’s exam, so you decide to use your ML theory knowledge to get through it.

There are two acceptable ways to write the digit ‘7’. It can be written with or without a line in the middle. Given an unlabelled dataset of 7s written in both ways, the task is to find which ones have a dash and which ones don’t.

Consider the following problem. There is an unknown discrete probability distribution on the alphabet \([K]\). Let this distribution be \(p=[p_1,p_2,..,p_K]\). The mode of this distribution is \(k^\star = \arg \max_{k \in [K]} p_k\) and let \(p^\star = p_{k^\star}\). You have access to a noisy oracle. The goal is to query this oracle for \(T\) rounds such that the following regret is minimized.

Recall the Babylonian method for computing square roots, which you might have learnt in highschool. I propose a higher dimensional variant of that, which I use to solve a few Non-Convex problems, specifically computing Matrix Square root, Positive Semidefinite matrix completion and Euclidean Distance Matrix completion.

Let \(X\) be a \(n\times k\) real matrix. It can be interpreted as \(n\) points, \(x_1,x_2,..x_n \in \mathbb{R}^k\). The Euclidean Distance Matrix(EDM) \(D\) is \([D]_{i,j} = \|x_i-x_j\|_2^2\). In the EDM completion problem, we are given some entries of \(D\) which are randomly sampled according to a probability \(p\). The goal is to determine the remaining entries of \(D\) and additionally the point matrix \(X\) producing \(D\). This is similar to the generic Low rank matrix completion problem, except on EDMs.

This is a follow up to my previous post: An Efron-Stein Like Lower bound for Variance, where I derived the following inequality.

In a homework of the Machine Learning Theory course that I am taking at UMass, we were asked to prove the Efron-Stein Inequality. It upper bounds the variance of arbitrary functions of iid random variables. While working on the proof, I found an intriguing inequality which has the structure of Efron-Stein, but is a lower bound.

This post is about finding the minimum and maximum eigenvalues and the corresponding eigenvectors of a matrix \(A\) using Projected Gradient Descent. There are several algorithms to find the eigenvalues of a given matrix (See Eigenvalue algorithms). Although I could not find Projected Gradient Descent in this list, I feel it is a simple and intuitive algorithm.

You are an intern at a prestigious AI lab. Assume there are \(n\) researchers in this lab. The lab is located at the origin of a metric space. The researchers live at various points in this space. Everyday, these researchers travel to the lab from their respective homes and back. Each researcher owns an eco-friendly motor bike which can carry at most 2 passengers. They decide to bike-pool to work such that the total distance traveled is minimized. They entrust you to come up with an algorithm which can find the optimal sharing scheme.

This post is about a simple yet very efficient Bayesian algorithm for minimizing cumulative regret in Episodic Fixed Horizon Markov Decision Processes(EFH-MDP). First introduced as a heuristic by Strens under the name of “Bayesian Dynamic Programming”, it was later shown by Osband et.al that it is in fact an efficient RL algorithm. They also gave it a more informative name - Posterior Sampling for Reinforcement Learning (PSRL).

This blog post is about Episodic Fixed Horizon Markov Decision Processes (EFH-MDP). MDPs are a very generic framework and can be used to model complex systems in manufacturing, control and robotics to state a few. These are also used to model environments in Reinforcement Learning (RL).

You are given \(N\) coins which may be biased. Whenever you toss a coin and get a Heads, you score a point. Now consider these two objectives:

This blog post is about Bayesian Inference. It finds extensive use in several Machine learning algorithms and applications. Bayesian Inference, along with Frequentist Inference are the two main approaches to Statistical Inference.

This blog post is about the Multi Armed Bandit(MAB) problem and about the Exploration-Exploitation dilemma faced in reinforcement learning. MABs find applications in areas such as advertising, drug trials, website optimization, packet routing and resource allocation.

Backpropagation is an algorithm used to train neural networks, used along with an optimization routine such as gradient descent. Gradient descent requires access to the gradient of the loss function with respect to all the weights in the network to perform a weight update, in order to minimize the loss function. Backpropagation computes these gradients in a systematic way. Backpropagation along with Gradient descent is arguably the single most important algorithm for training Deep Neural Networks and could be said to be the driving force behind the recent emergence of Deep Learning.

The purpose of this post is to serve as a very basic introduction to Concentration Inequalities. Concentration inequalities deal with deviations of functions of independent random variables from their expectation. These inequalities are used extensively in Machine Learning Theory for deriving PAC like results.

This post is about a neat application of Gödel numbering. This post is inspired by a question my friend was asked during an interview for Microsoft.

Linear Programming(LP) is a widely used technique in algorithm design and analysis, especially for getting good approximations for NP hard problems. The first step in LP would be to formulate the the problem as an optimization problem with linear constraints where the quantity we are trying to optimize is also linear. It is a good excersize to formulate simple problems as linear programs. Linear programming problems typically expressed in their canonical form look like this:

This post is about reconstructing the Minimum Spanning Tree(MST) of a graph when the weight of some edge changes.

This post will be about simple linear regression. I will first use calculus to derive an expression. Then I derive same expression in a more intuitive way using linear algebra.

This post will be about using Randomization for constructing Binary Search Trees (BST) whose worst case height must be \(O(\log n)\). This post is inspired from a question I was asked in my B.Tech Grand Viva.

This is my first blog post. In this blog, I would be writing about Algorithms, Machine Learning, Optimization and Mathematics. I wanted to begin with something simple, so this post would be about a problem from Probability.