Matrix Multiplication as Tensor Decomposition

The recent paper, Discovering faster matrix multiplication algorithms with reinforcement learning by DeepMind, has been garnering much attention from both the ML and TCS communities. The algorithm in the paper, called AlpaTensor, can find fast matrix multiplication algorithms for some fixed-size matrices. Some in the ML community hail it as yet another outstanding achievement for deep RL :

On the other hand, the TCS community has a slightly different opinion about the work:

Since matrix multiplication is so pervasive in modern computing, the paper claims that these new algorithms could lead to a 10-20% improvement across trillions of calculations.

However, its applicability might be limited due to the algorithms being numerically unstable:

In any case, I thought the paper was cool, and I learned a new trick because of it:

Matrix multiplication can be represented as a Tensor. A tensor decomposition for this tensor with the least number of terms gives the fastest algorithm for multiplying matrices.

Let \(A\in \mathbb{R}^{m \times n}\) and \(B \in \mathbb{R}^{n \times p}\). Let \(C\in \mathbb{R}^{m\times p}\) be the product \(C=AB\). Let \(\phi_i: \mathbb{R}^{m \times n} \to \mathbb{R}\) and \(\psi_i: \mathbb{R}^{n \times p} \to \mathbb{R}\) be linear operators and \(W_i \in \mathbb{R}^{m \times p}\). Consider the map \(M_{m,n,p}: \mathbb{R}^{m \times n} \times \mathbb{R}^{n \times p} \to \mathbb{R}^{m\times p}\):

\[M_{m,n,p}(A,B) = \sum_{i=1}^r \phi_i(A)\psi_i(B) W_i\]

The goal is to find \(r\) triplets \((W_i, \phi_i,\psi_i)\) such that \(M_{m,n,p}(A,B) =AB\) for all matrices \(A,B\). Then:

\[\begin{align*} C[u,v] &= \sum_{i=1}^r W_i[u,v] \phi_i(A)\psi_i(B)\\ &= \sum_{i=1}^r W_i[u,v]\left(\sum_{u',v'} \phi_i[u',v']A[u',v'] \right) \left(\sum_{u'',v''} \psi_i[u'',v'']B[u'',v''] \right)\\ &= \sum_{i=1}^r \sum_{(u',v'),(u'',v'')} W_i[u,v]\phi_i[u',v'] \psi_i[u'',v''] A[u',v'] B[u'',v''] \\ &= \sum_{i=1}^r\sum_{(u',v'),(u'',v'')} T_i[(u,v),(u',v'),(u'',v')] A[u',v'] B[u'',v''] \end{align*}\]

Let \(T_i\) be the rank 1 tensor \(T_i = W_i \otimes \phi_i \otimes \psi_i\). Then \(T = \sum_{i=1}^r T_i\) is the matrix multiplication tensor. An algorithm for matrix multiplication is given by the tensor decomposition \(T=\sum_{i=1}^r T_i\), and it consists of \(r\) multiplication steps.

Why is this a difficult problem?

Let us make things less cumbersome and only consider the case of square matrices, i.e., \(m=n=p\). In this case \(T\) would be an \(n^2 \times n^2 \times n^2\) tensor. We can compute \(T\) by simply using the definition of matrix multiplication :

\[\begin{align*} C[u,v] &= \sum_{i=k}^n A[u,k][B[k,v]\\ &= \sum_{(u',v'),(u'',v'')} 1(u'=u,v''=v,v'=u'') A[u',v'] B[u'',v''] \end{align*}\]

This also tells us that \(T\) can be decomposed as a sum of \(n^3\) rank 1 tensors. Finding the most efficient matrix multiplication algorithm boils down to finding a decomposition with the least number of rank 1 tensors. This number is also the rank of the tensor \(T\).

So we know what \(T\) looks like. For instance, when \(n=2\), the tensor \(T\) is shown below (taken from the paper). Here a filled in box has value 1 and the rest of the boxes are 0:

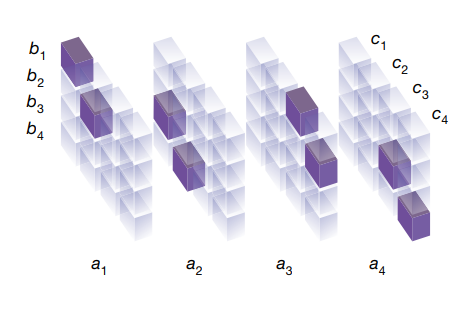
tensor

What stops us from computing its decomposition and creating the most efficient matrix multiplication algorithm? Unlike matrix rank-decomposition, which is relatively easy to compute using techniques like SVD, tensor rank-decomposition is an NP-Complete problem.[1]. For \(2\times 2\) matrices, Strassen’s algorithm requires \(7\) multiplications, whereas the schoolbook algorithm needs \(8\). The rank of the matrix multiplication tensor for the \(2\times 2\) case was proven to be \(7\) in [2], showing that Strassen’s algorithm is optimal. For the \(3\times 3\) case, the rank is still unknown. However, upper and lower bounds are known. For more details, see [3].

How does the DeepMind paper solve this?

Finding the tensor decomposition is formulated as a single-player game. The state of the game is given by \(S_t\), which is initialized as \(S_0=T\). At each step, the player guesses a triplet \((W_t, \phi_t,\psi_t)\) and the next state is given by \(S_{t} = S_{t-1} - W_t \otimes \phi_t \otimes \psi_t\). The game ends when \(S_t=0\). The game rewards are set up so that the player tries to reach \(S_t=0\) in as few steps as possible. If the game ends, the sequence of guesses \((W_t, \phi_t,\psi_t)_{t=1}^R\) constitute an \(R\) rank-decomposition of \(T\). The rest of the paper deals with all the engineering required to solve this game.

Given a decomposition \(T = \sum_{i=1}^R W_i \otimes \phi_i \otimes \psi_i\), the matrix product \(C=AB\) can be computed as below (same as Algorithm 1 in the paper):

  1. First compute \(m_i = \phi_i(A) \psi_i(B) = \left(\sum_{u',v'} \phi_i[u',v']A[u',v'] \right) \left(\sum_{u'',v''} \psi_i[u'',v'']B[u'',v''] \right)\) for \(i=1,\dots, R\). So, there are a total of \(R\) multiplications.
  2. Combine to get \(C = \sum_{i=1}^R W_i m_i\)

TL;DR

The procedure for multiplying two \(n\times n\) matrices can be encoded as a \(3\)-order tensor. An efficient algorithm for matrix multiplication can be found by searching through the space of rank 1 tensors for a decomposition of the matrix multiplication tensor. RL is just a technique used for searching through this space.

I recall another paper that uses RL to find an efficient algorithm. See, for instance, the paper Reinforcement Learning for Integer Programming: Learning to Cut[4], which uses RL to find cutting planes.

References:

  • [1] Johan, Hastad. “Tensor Rank is NP-complete.” Journal of Algorithms 4.11 (1990): 644-654.
  • [2] Landsberg, J. “Geometry and the complexity of matrix multiplication.” Bulletin of the American Mathematical Society 45.2 (2008): 247-284.
  • [3] E0309 Topics in Complexity Theory, Lecture 3, Neeraj Kayal, Abhijat Sharma https://www.csa.iisc.ac.in/~chandan/courses/arithmetic_circuits/notes/lec3.pdf
  • [4] Tang, Yunhao, Shipra Agrawal, and Yuri Faenza. “Reinforcement learning for integer programming: Learning to cut.” International conference on machine learning. PMLR, 2020.

Anything wise in these pages you should credit to the many experts who preceded me. Anything foolish, assume it is my error - James Clear

Written on October 8, 2022