Learning the Mode under Bandit Feedback
Consider the following problem. There is an unknown discrete probability distribution on the alphabet \([K]\). Let this distribution be \(p=[p_1,p_2,..,p_K]\). The mode of this distribution is \(k^\star = \arg \max_{k \in [K]} p_k\) and let \(p^\star = p_{k^\star}\). You have access to a noisy oracle. The goal is to query this oracle for \(T\) rounds such that the following regret is minimized.
\[Regret(T) = Tp^\star - \sum_{t=1}^T p_{k_t}\]We consider two kind of oracles, \(O_1\) and \(O_2\). The first oracle \(O_1\) outputs a \(k \in [K]\) according to probability \(p_k\). The second oracle \(O_2\) says \(k\) is the mode with probability \(p_k\), ie, \(O(k) = 1\) with probability \(p_k\) and \(O(k) = 0\) with probability \(1-p_k\).
For \(O_1\), I present a simple Bayesian algorithm which outperforms vanilla Thompson Sampling. For \(O_2\), Thompson sampling works, but can we do better?
Oracle \(O_1\)
When \(O_1\) is queried, it outputs a sample according to the unknown distribution \(p\). This oracle can be considered as a noisy answer to the question “Who is the mode?”. This problem can be solved by treating it as a Multi Armed Bandit. The basic Beta-Bernoulli version of Thompson sampling (TS) can be used by deciding the reward to give at each round. Say we pull \(k_t\) at round \(t\) and the oracles outputs \(k_{O}\), then the reward \(r=1\) if \(k_t=k_{O}\) or is \(0\) otherwise. We use a Beta prior for each \(p_k\) and a Bernoulli likelihood for the reward.

Since the oracle outputs one of \([K]\) at each round, it can be seen as producing a categorical random variable. Also, since the probabilities \(p_k\) sum to \(1\), a single Dirichlet prior can be used instead of \(K\) Beta priors. We can use a categorical version of TS, which uses the Dirichlet-Categorical conjugate pair.

I created a probability distribution on \([10]\) and ran the two algorithms for 10000 steps, 100 times. Here is the regret plot with confidence intervals.
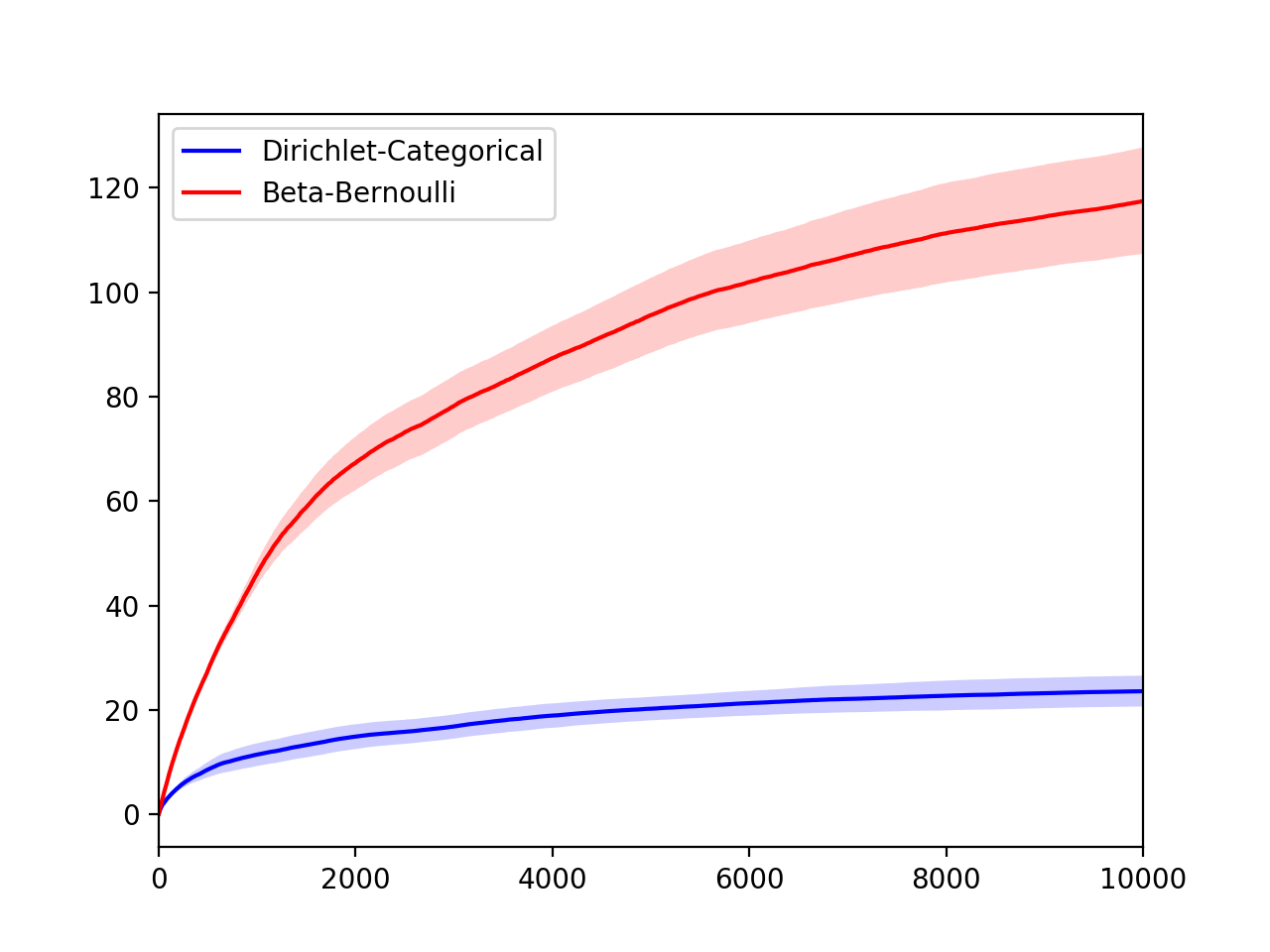
The second algorithm performs better because it uses all the information that the oracle provides and also uses a better prior.
Oracle \(O_2\)
This oracle is not as informative as \(O_1\). It has to be queried with a \(k\in [K]\) and it outputs \(1\) with probability \(p_k\), and \(0\) otherwise. It can be considered as a noisy answer to the question “Is k the mode?”. We can again treat this as a Multi Armed Bandit problem. The Beta-Bernoulli version of TS can be used by using the output of the oracle as the reward for pulling that arm. The algorithm is:

Although this algorithm works, I believe it is possible to do better. This is because it does not use the fact that \(\sum_{k=1}^K p_k= 1\). We cannot apply the Dirichlet version of TS as the likelihood in this case is Bernoulli and not Categorical.
Let \(S\) be the \(K-1\)-simplex(set defined by \(\{[p_1,p_2,.p_K]: p_k\geq 0 \text{ and } \sum_{k=1}^K p_k=1\}\)). Consider the following probability distribution:
\[\begin{align} f(p,\alpha,\beta) &= \prod_{k=1}^K p_k^{\alpha_k-1}(1-p_k)^{\beta_k-1}\\ Z(\alpha,\beta) &= \int_{S} f(p,\alpha,\beta) dp_1dp_2..dp_K\\ \Pr(P=p; \alpha,\beta) &= \frac{f(p,\alpha,\beta) }{Z(\alpha,\beta)} \end{align}\]This distribution will be a Conjugate prior to a Bernoulli likelihood. We can design a TS algorithm which uses this conjugate pair. The posterior update will look something like this:
\[\begin{align} \Pr(p|r) &= \frac{\Pr(r|p) \Pr(p)}{\Pr(r)} = \frac{p_{k_t}^r (1-p_{k_t})^{1-r }f(p,\alpha,\beta)}{\int_S p_{k_t}^r (1-p_{k_t})^{1-r }f(p,\alpha,\beta)}\\ &= \frac{f(p,\alpha',\beta')}{Z(\alpha',\beta')} = \Pr(P=p; \alpha',\beta') \end{align}\]Here \(\alpha_{k_t}' = \alpha_{k_t} + r, \beta_{k_t}' = \beta_{k_t} + 1-r\) and all other \(\alpha_k, \beta_k\) remain unchanged.
However, I have not been able to find a procedure which draws samples from this distribution. Please let me know if you have seen this distribution before or if there is a way to draw samples from it.
What can we do in the case where the probability distribution is continuous with support on a closed convex set?