Bregman Lower Bounds and Regret Inequalities
So far, we have shown how to get regret inequalities for OMD/FTRL where the second term is a sum, whose summands are of the form:
\[l^\top(x-y)-\frac{1}{\eta} \text{Breg}(y\|x)\]Say we have a lower bound on the Bregman:
\[\text{Breg}(y\|x) \geq h_x(x-y)\]Then, we can bound the term as:
\[\begin{align*} l^\top(x-y)-\frac{1}{\eta} \text{Breg}(y\|x) &\leq l^\top(x-y) - \frac{1}{\eta}h_x(x-y) \\ &\leq \frac{1}{\eta} \sup_{a \in \mathbb{R}^n} \left[\eta l^\top a - h_x(a)\right]\\ &= \frac{h_x^\star(\eta l)}{\eta} \end{align*}\]The subscript \(x\) in \(h_x\) emphasizes that the lowerbound function may depend on \(x\). The convex conjugate of \(h_x\) is \(h_x^\star\).
For example, if \(\psi = \exp\), then \(f=x\log x-x\) and \(\text{Breg}\) will be the KL divergence. Then, we readily have a lowerbound through Pinsker’s inequality:
\[KL(y\|x) \geq \frac{1}{2} \|y-x\|_1^2\]This would imply a regret bound:
\[l^\top(x-y)-\frac{1}{\eta} KL(y\|x)\leq \frac{\eta}{2} \|l_t\|_\infty^2\]For any potential \(\psi\), if one can show a quadratic lowerbound:
\[\text{Breg}(y\|x) \geq \frac{1}{2}(x-y)^\top M(x)^{-1}(x-y)\]This would imply a regret bound:
\[l^\top(x-y)-\frac{1}{\eta} \text{Breg}(y\|x)\leq \frac{1}{2\eta} (\eta l)^\top M(x)(\eta l) = \frac{\eta}{2} l^\top M(x)l\]In the remaining post, I prove a neat theorem.
Lemma Let \(p=\psi(a)\) and \(q=\psi(b)\). Let \(\phi\) be a positive function such that \(b \leq a+\phi(a)\) and define
\[m(a) = (\psi(a+\phi(a))-\psi(a))/\phi(a)\]Then, we have the lowerbound:
\[\text{Breg}(q\|p) \geq \frac{1}{2} \frac{(p-q)^2}{m(\psi^{-1}(p))}\]Proof
Using properties of potential functions, we know that:
\[{f^\star}'(a) = \psi(a) \quad \text{ and } \quad \int_{\infty}^a \psi(x) dx = f^\star(a)\]Using properties of conjugate duality and Bregman, we have:
\[\begin{align*} \text{Breg}(q\|p) &= \text{Breg}(\psi(b)\|\psi(a)) = \text{Breg}^\star(a\|b) = f^\star(a)-f^\star(b)- {f^\star}'(b)^\top(a-b) \end{align*}\]We can visualize this quantity using potential functions.
Case1: \(a\geq b\)
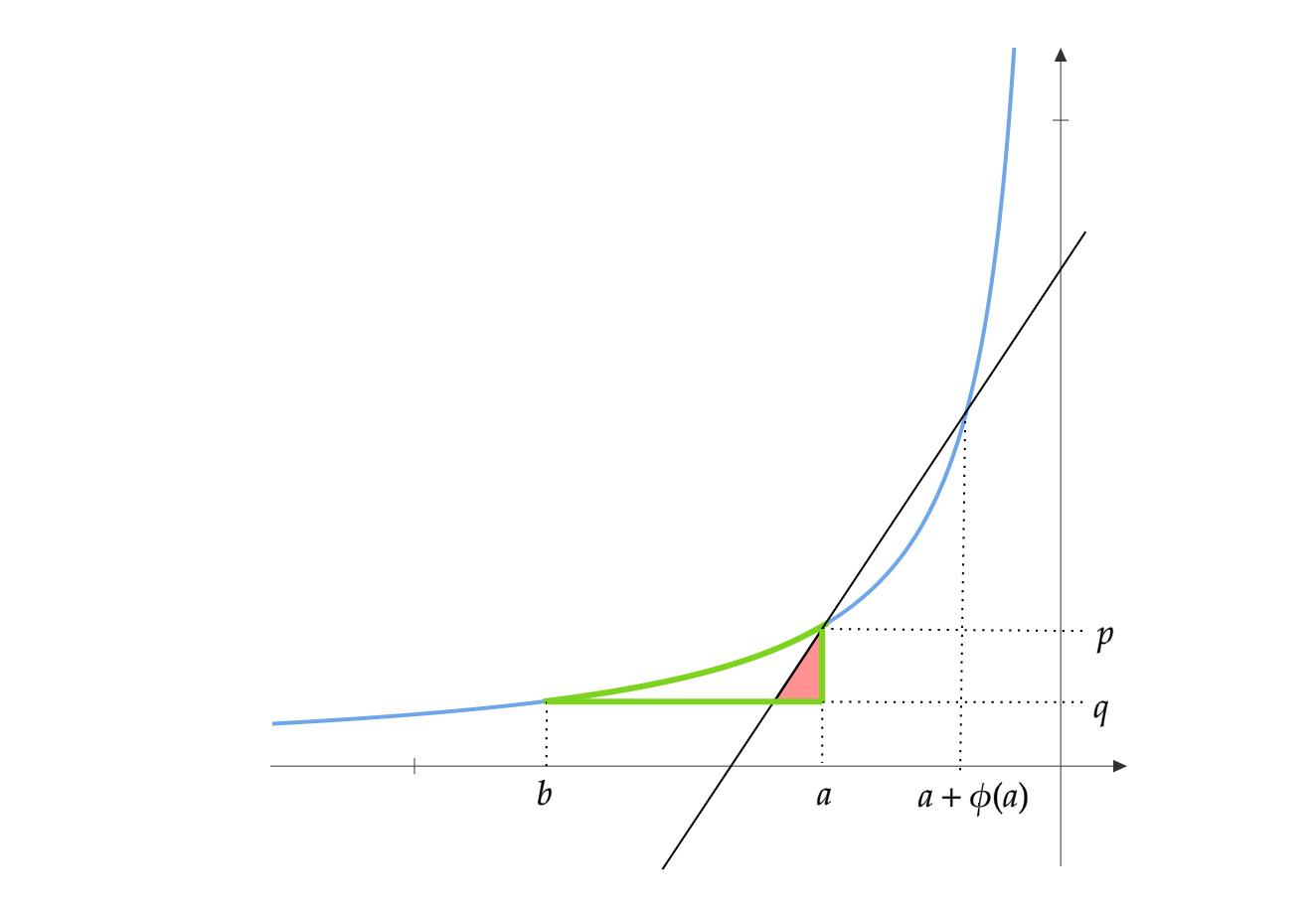
Since \(f^\star(a)\) is the integral of \(\psi\), it is the area below the curve before \(a\). Similarly \(f^\star(b)\) is the area below the curve before \(b\). The area of rectangle \((b,a)\times(0,q)\) is given by \({f^\star}'(b)(a-b) = q(b-a)\).
So \(f^\star(a) - f^\star(b) - {f^\star}'(b)(a-b)\) is the area with green borders.
Consider the line which intersects the curve at \((a,p)\) and \((a+\phi(a),\psi(a+\phi(a)))\). The slope of this line is
\[m(a) = \frac{\psi(a+\phi(a)) - \psi(a)}{\phi(a)}\]Consider the red triangle in the figure. Its height is \((p-q)\). Using similar triangles, its base length is \((p-q)/m(a)\). So, the red triangle has area:
\[\frac{1}{2} \frac{(p-q)^2}{m(a)} = \frac{1}{2} \frac{(p-q)^2}{m(\psi^{-1}(p))}\]Since this is clearly smaller than the area enclosed in green, we have:
\[\text{Breg}(q\|p) \geq \frac{1}{2} \frac{(p-q)^2}{m(\psi^{-1}(p))}\]Case2: \(a\leq b \leq a+\phi(a)\)
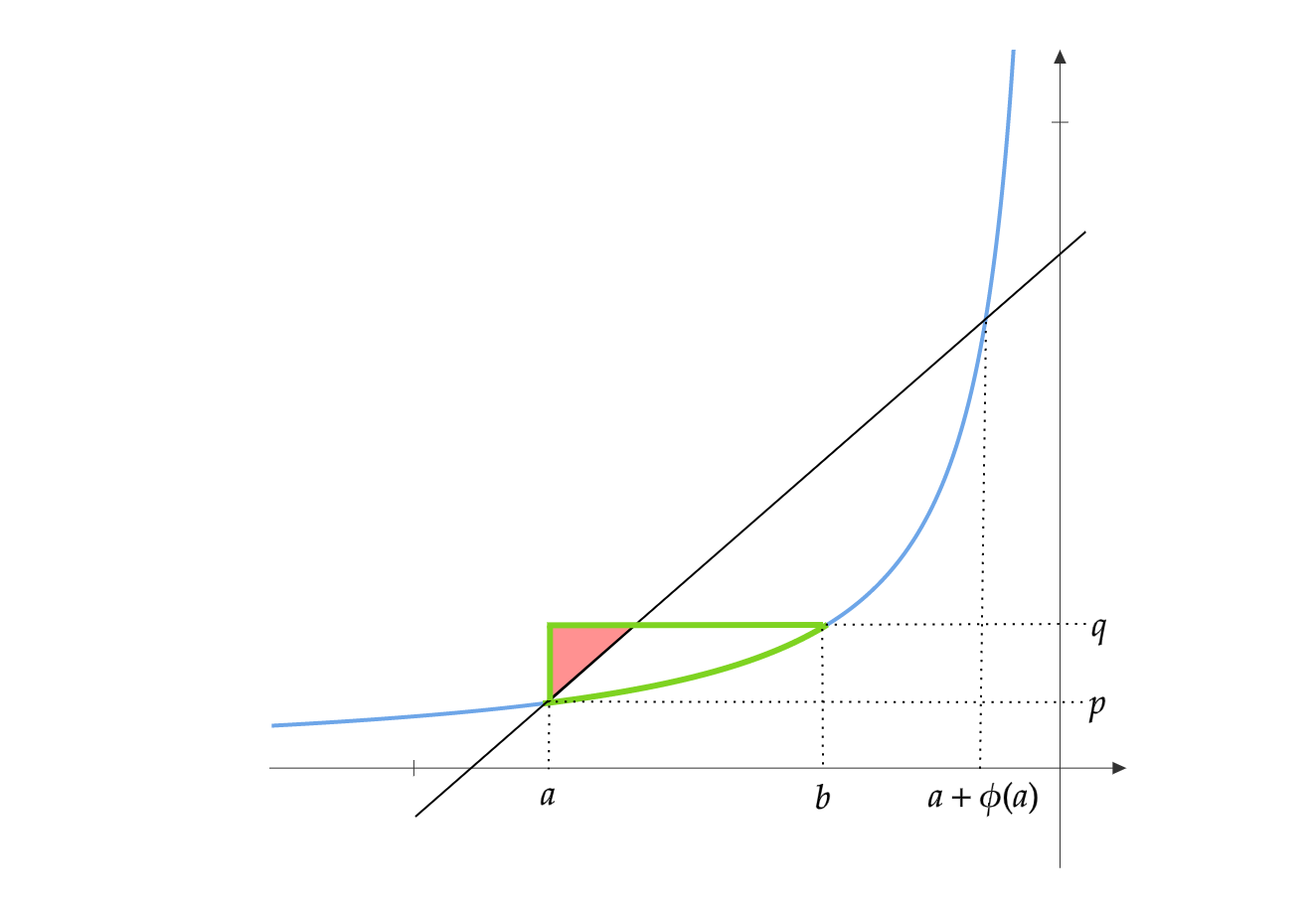
We can repeat the same argument with the figure above. The area of the red triangle is smaller than the area enclosed in green. This gives:
\[\text{Breg}(q\|p) \geq \frac{1}{2} \frac{(p-q)^2}{m(\psi^{-1}(p))}\]Q.E.D
Theorem
Let \(x = \psi(u)\), \(y=\psi(v)\). Then, we have the lowerbound:
\[\text{Breg}(y\|x) \geq \frac{1}{2} \sum_{i=1}^n \frac{(x_i-y_i)^2}{m(\psi^{-1}(x_i))}\]This would imply a regret bound:
\[l^\top(x-y)-\frac{1}{\eta} \text{Breg}(y\|x)\leq \frac{\eta}{2} \sum_{i=1}^n l_i^2 m(\psi^{-1}(x_i))\]Proof
Using properties of conjugate duality and Bregman, we have:
\[\begin{align*} \text{Breg}(y\|x) &= \text{Breg}(\psi(v)\|\psi(u)) = \text{Breg}^\star(u\|v) = F^\star(u)-F^\star(v)-\nabla F^\star(v)^\top(u-v)\\ &= \sum_{i=1}^n f^\star(u_i) - f^\star(v_i) - {f^\star}'(v_i)(u_i-v_i) \geq \frac{1}{2} \sum_{i=1}^n \frac{(x_i-y_i)^2}{m(\psi^{-1}(x_i))} \end{align*}\]The second statement is easy to verify from this point.
Q.E.D
Corollary
If \(y\leq x\) then by we have the lowerbound:
\[\text{Breg}(y\|x) \geq \frac{1}{2} \sum_{i=1}^n \frac{(x_i-y_i)^2}{\psi'(\psi^{-1}(x_i))}=\frac{1}{2} \sum_{i=1}^n (x_i-y_i)^2 f''(x_i)\]This would imply a regret bound:
\[l^\top(x-y)-\frac{1}{\eta} \text{Breg}(y\|x)\leq \frac{\eta}{2} \sum_{i=1}^n \frac{l_i^2}{f''(x_i)}\]Proof
Since \(y\leq x\), we only have to invoke Case 1 from the lemma above. Applying the limit on functions \(\phi(u) \to 0\), we can see that \(m(u)\to \psi'(u)\)
Parts of this post appear in my paper : Putta, S. R., & Agrawal, S. (2021). Scale Free Adversarial Multi Armed Bandits. arXiv preprint arXiv:2106.04700.
