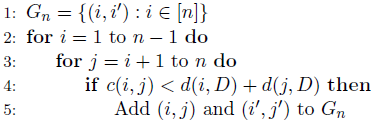Perfect Matchings : Optimal Bike-pooling for a Common Destination
You are an intern at a prestigious AI lab. Assume there are \(n\) researchers in this lab. The lab is located at the origin of a metric space. The researchers live at various points in this space. Everyday, these researchers travel to the lab from their respective homes and back. Each researcher owns an eco-friendly motor bike which can carry at most 2 passengers. They decide to bike-pool to work such that the total distance traveled is minimized. They entrust you to come up with an algorithm which can find the optimal sharing scheme.
Lets start with the simple case of just 2 researchers who stay at \(X\) and \(Y\). The lab is located at \(D\). Let \(d\) be the distance metric in this space.

There are three choices here:
- \(X\) goes to \(Y\) and then \(X\),\(Y\) travel to \(D\). \(cost = d(X,Y) + d(Y,D)\)
- \(Y\) goes to \(X\) and then \(X\),\(Y\) travel to \(D\). \(cost = d(X,Y) + d(X,D)\)
- \(X\) and \(Y\) travel to \(D\) separately. \(cost = d(X,D) + d(Y,D)\)
Let \(c(X,Y)\) be the total distance traveled when \(X\) and \(Y\) decide to bike-pool.
\[c(X,Y) = d(X,Y) + min(d(X,D),d(Y,D))\]It makes sense to bike pool only if \(d(X,D) + d(Y,D) > c(X,Y)\). Consider the Minimum Weight Perfect Matching (MWPM) of this graph (This will be useful later):

This graph has 2 perfect matchings, \(\{XX',YY'\}\) and \(\{XY,X'Y'\}\) with weights \(d(X,D) + d(Y,D)\) and \(c(X,Y)\) respectively. The MWPM of this graph will be one of these two sets depending on which one has a smaller weight. If it is \(\{XX',YY'\}\), then \(X\) and \(Y\) should travel separately. If it is \(\{XY,X'Y'\}\), then they should pool.
For the case of \(n\) researchers, construct a weighted graph \(G_n\) which consists \(2n\) vertices and \(n^2\) edges. The vertex set is \(\{1,2,..,n\} \cup \{1',2',..,n'\}\). Graph \(G_n\) is composed of two complete graphs \(K_n\), \(K_n'\) and edges connecting corresponding vertices, i.e, edges \(\{(i,i'): i \in [n]\}\), which we call as cross edges. For instance, \(G_4\) would look something like this:

The weights are defined as follows: \(w(i,j) = w(i',j') = \frac{c(i,j)}{2} \quad \text{and} \quad w(i,i') = d(D,i)\)
The graph \(G_n\) is guaranteed to have to have at least one perfect matching. A minimum weight perfect matching for this graph can be found using the Blossom algorithm of Edmonds. Assume there is a unique minimum weight perfect matching \(M\). The following theorem states that the matching is always symmetric.
Theorem: \((i,j) \in M\) if and only if \((i',j') \in M\)
Proof: The matching can be written as \(M=A \cup B \cup C\). \(A\), \(B\) and \(C\) are the sets of matching edges belonging to \(K_n\), \(K_n'\) and the crossing edges respectively. \(A\),\(B\) and \(C\) are disjoint. Let \(w(E)\) is the weight of the edges in edges set \(E\).
Assume there exists some \((i,j) \in A\) such that \((i',j') \notin B\) or some \((i,j) \notin A\) such that \((i',j') \in B\).
Since \(A\) and \(B\) differ in atleast 1 edge and a unique minimum weight perfect matching exists, \(w(A) \neq w(B)\). Without loss of generality, let \(w(A)<w(B)\)
The weight of the minimum weight perfect matching is: \(w(M) = w(A) + w(B) + w(C)\)
Consider the set \(A' = \{(i',j'):(i,j) \in A\}\). Clearly \(w(A)=w(A')\). The set \(A \cup A' \cup C\) is also a perfect matching of \(G\). But \(w(A) + w(A') + w(C) < w(A) + w(B) + w(C)\).
We arrive at a contradiction. Hence, for all \((i,j) \in A\), \((i',j') \in B\) and vice-versa. Hence \((i,j) \in M\) if and only if \((i',j') \in M\).
In the case where there exist multiple minimum weight perfect matchings, Blossoms may output a non-symmetric matching \(M = A \cup B \cup C\). But, \(w(A)=w(B)=w(A')\). Hence \(A \cup A' \cup C\) will also be a minimum weight perfect matching. Hence, once \(M\) is found, the optimal way to bike-pool can be extracted easily. If \((i,j) \in M\) then \(i\) and \(j\) must bike-pool. In the other case when \((i,i') \in M\), \(i\) must go directly to \(D\).
Complexity
Edward’s Blossom algorithm itself deserves a separate post. On a graph with \(n\) vertices and \(m\) edges, a straight forward implementation of the Blossom algorithm has a complexity of \(O(n^2m)\). Gabow showed a bound of \(O(n(m+n \log n))\), which is currently the best known result. A fast implementation of the Blossom algorithm called Blossom V could be used for finding the MWPM.
For our bike-pooling problem, the complexity would be \(O(n^2)\) for constructing \(G_n\) and \(O(2n(n^2+2n \log 2n)) = O(n^3)\) for running blossom on this graph. This can be improved by the following observation: There may be a lot of redundant edges in \(G_n\) which can be pruned off.
Let \(D\) be the destination and \(X\), \(Y\) be two researchers. If we fix the position of \(D\) and \(Y\), what is the region where \(X\) could lie such that \(Y\) goes to \(X\) and then \(X\),\(Y\) travel to \(D\).
The two conditions that must be satisfied are:
- \[d(X,D)<d(Y,D)\]
- \[c(X,Y)<d(X,D) + d(Y,D) \implies d(X,Y) < d(Y,D)\]
The feasible region is the gray area:

We can use this condition to construct \(G_n\) such that it has only the required number of edges:
The resulting graph \(G_n\) will still have perfect matchings and the above theorem will still hold. If \(G_n\) has \(2m+n\) edges, the complexity of the bike-pooling problem is :
\[O(n^2 + 2n(2m+n + 2n \log 2n)) = O(n(m+n \log n))\]This could still be \(O(n^3)\) in the worst case when \(O(m) = O(n^2)\).
Visualization
To visualize the solution, I created 10 random positions for the researchers in the 2D plane. You can find the code here.
In this instance, everyone gets matched.
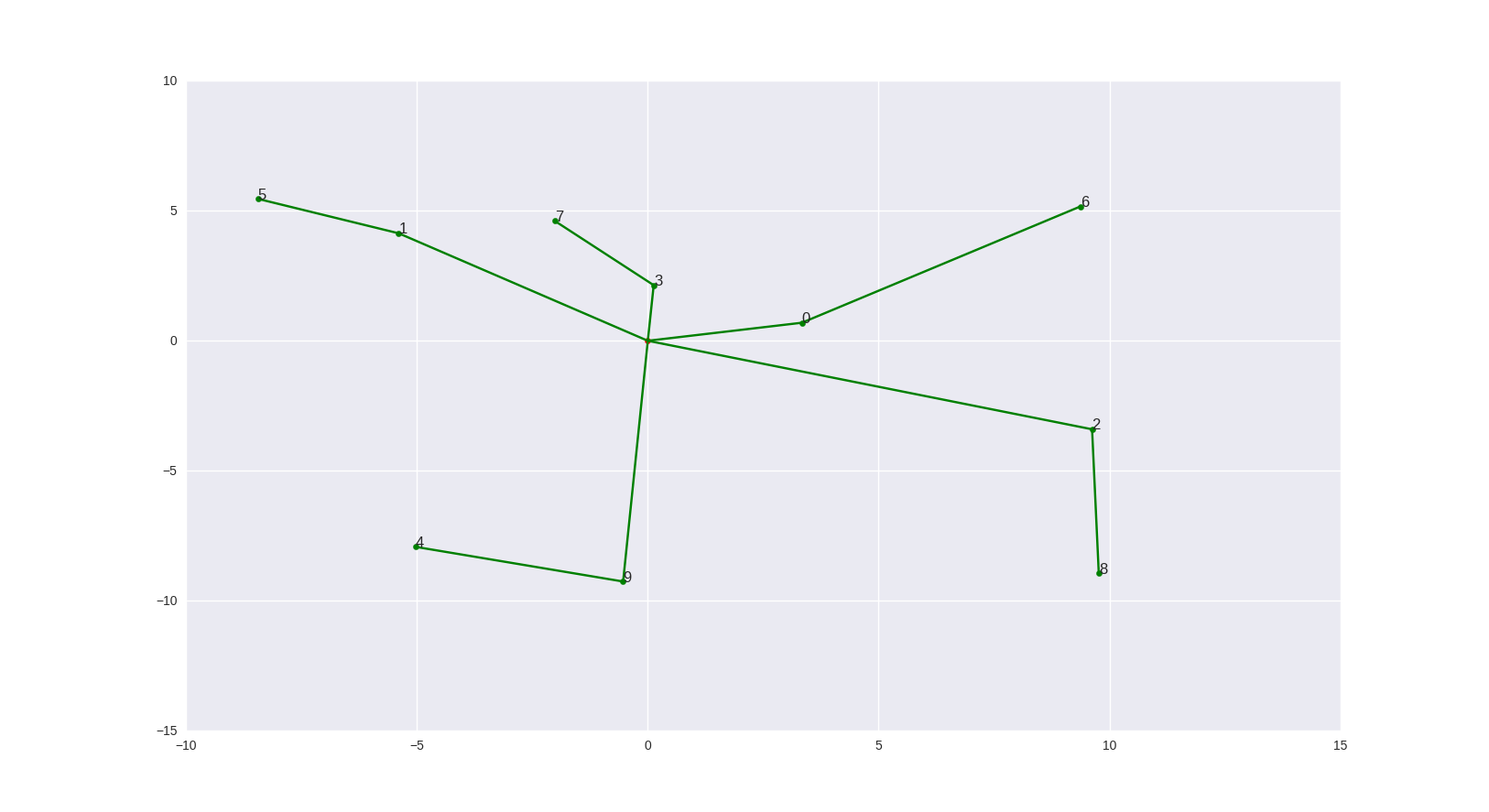
In this instance, (6,6’) and (9,9’) get matched. So 6 and 9 travel alone.
What about car pooling?
For capacity larger than 2, the problem will involve general Hypergraph Matching, which is NP-hard. We could look for approximation algorithms. If you have an idea for car pooling, please get in touch.